Addierer - Digitale Mathematik

 

Materialbedarf

 

Anz. Bezeichnung Datenblatt
1 Batterie/Spannungsquelle 9V  
1 CMOS-IC 4070
1 CMOS-IC 4071
1 CMOS-IC 4081
2 Widerstand 470 Ohm  
3 Widerstand 1,0 MOhm  
3 Mikrotaster
2 Standard-Leuchtdiode 3mm oder 5mm 3mm, 5mm

 

 

Grundlagen

 

Digitale Schaltungen werden unter anderem oft dort eingesetzt, wo man bestimmte Berechnungen anstellen muss. Auch jeder Computer funktioniert im Grunde nur, weil dieser rechnen kann. Aber, wie rechnet man in der Digitaltechnik? Dazu schauen wir uns anhand einer Tabelle einmal an, welche Bedingungen im Binärsystem erfüllt sein müssen, damit wir zwei Zahlen addieren können.

 

Summand A + Summand B

 Summe Übertrag
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1

 

Betrachten wir diese Tabelle genauer, sehen wir, dass sich in dieser Tabelle 2 Logikfunktionen verbergen. Die Summe können wir mit Hilfe eines Exklusiv-Oder-Gatters nachbilden und den Übertrag gestalten wir mit einem Und-Gatter.

 

 

Der Halbaddierer

 

 

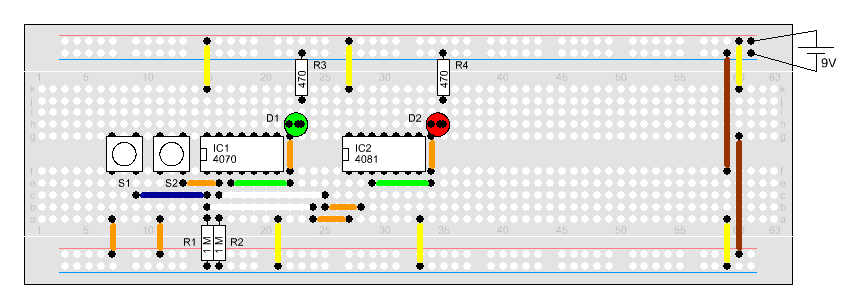
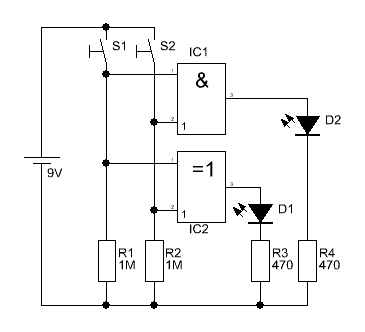
Hier können wir nun, bei der Inbetriebnahme, sehr gut testen, wie man zwei Binärwerte mit Hilfe dieser kleinen digitalen Schaltung addiert.

Ist keiner der beiden Taster betätigt, sind auch die beiden Leuchtdiode aus. Wird einer der beiden Taster S1 oder S2 betätigt, leuchtet die LED D1 auf, da 0+1 oder 1+0 im Binärsystem 1 ergibt. Einen Übertrag entsteht nicht, daher bleibt die Leuchtdiode D2 dunkel.

Drücken wir beide Taster ist die Summe 0, d.h. die LED D1 ist aus. Aber hier entsteht nun ein Übertrag an die nächste Binärstelle. Dies wird durch D2 angezeigt.

 

 

2 x Halbaddierer = 1 Volladdierer

 

Bei der kleinen Schaltung eben, konnten wir sehr schön beobachten, wie man 2 Binärwerte miteinander addiert. Aber, wir haben hierbei ein großes Problem. In der Regel besteht eine Rechenschaltung nicht nur aus 1 Bit pro Wert am Eingang, sondern wir haben 4, 8 oder mehr Bits die parallel addiert werden müssen. Dabei muss der Übertrag der niederwertigeren bei der Addition der nächsten Stufe mit berücksichtig werden. Aber unsere Schaltung besitzt hierfür keinen Eingang.

 

Um dies zu erreichen müssen wir das Ergebnis der 'normalen' Addition im Grunde noch einmal mit dem Übertragsbits der vorhergehenden Stufe verknüpfen. Wir brauchen also noch eine Additionsstufe.

 

 

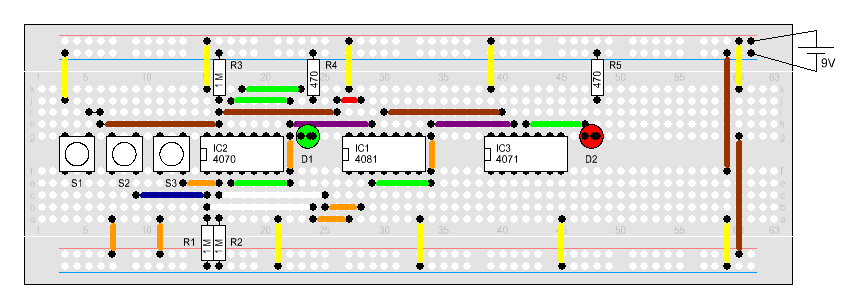
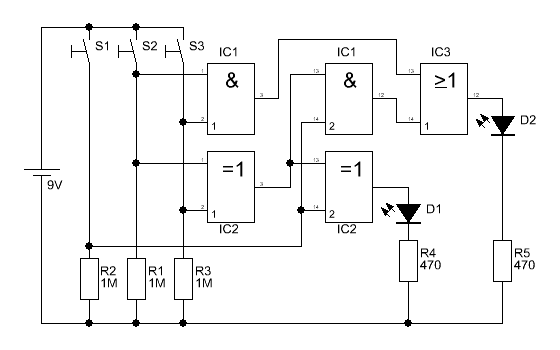
Im Schaltplan kann man nun gut erkennen, dass wir noch eine weitere Additionsstufe hinzugefügt haben. S1 stellt hierbei die Simulation des Übertragsbits der letzten Stufe dar.

Da wir nun 2 Bits + Übertrag komplett berechnen können, wird diese Schaltung auch Volladdierer genannt. Die Schaltung aus dem letzten Versuch kann ja nur die Hälfte der Addition, daher wird so ein Aufbau als Halbaddierer bezeichnet.

 

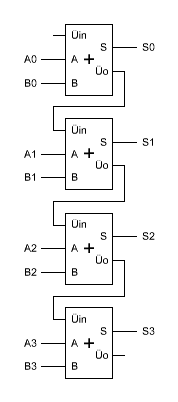Will man nun größere Additionsschaltungen aufbauen, muss man nur mehrere Volladdierer nehmen und diese so verschalten wie es im Prinzipschaltbild nebenan zu sehen ist. Dieser Aufbau lässt sich, wie man leicht erkennen kann, beliebig ausbauen.

Solche Volladdierer sind auch die wichtigsten Teile eines jeden Mikrocomputers. Dort findet man Rechenwerke, die ohne Probleme 32 oder 64 Bit verarbeiten können. Wer sich in Maschinenprogrammierung von Mikrokontrollern übt, wird auch ständig über das Übertragsbit stolpern. Dies spielt eine entscheidende Rolle bei der Programmierung. Beim Computer nennt man dieses Bit Carry-Bit.

 

 

Zurück zur Auswahlseite            Zur Hauptseite