Digitale Gesetze - Urteil folgt sofort

 

Digitale Schaltungen sind im Grunde ganz einfach. Sie können nur 2 Signale verarbeiten und bestehen aus nur wenigen kleinen Baugruppen, den Gattern. Doch, so einfach dies im ersten Moment scheint, gibt es auch hier die andere Seite der Medaille. Das Zusammenspiel der einzelnen logischen Gattern, sind einigen Gesetzen unterworfen, welche man kennen sollte. Durch diese Gesetze kann man sowohl Fehler vermeiden als auch Schaltungen optimieren.

 

Diese Gesetze sollen hier einmal vorgestellt werden.

 

 

Dualitätsgesetz

 

Im Dualitätsgesetz findet man nur die Begebenheit, dass, wenn man ein digitales ändert, sich der entsprechende andere Signalpegel ergibt. Aus einer 0 wird eine 1, ein 1-Signal wird zur 0.

 

 

Involutionsgesetz

 

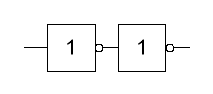Das Involutionsgesetz besagt, das zwei hintereinander geschaltete Inverter immer den Eingangswert wieder geben. Diese Schaltungsvariante scheint im ersten Moment unsinnig zu erscheinen. Aber sie wird doch hin und wieder angewendet.

Zum Beispiel um übrig gebliebene Inverter eines Schaltkreises nicht offen zu lassen. Oder, es wird, mit dieser Schaltung, ein Eingangssignal nochmals gefiltert um das Signal 'digitaler' zu machen. Eine weitere Anwendung sind Verzögerungsschaltungen. Durch die Signallaufzeit kann man das Eingangssignal, je nach Logikfamilie, um einige nS heraus zögern.

Ein ähnliches Gesetz gibt es auch für ODER oder UND-Gatter.

 

 

Idempotenzgesetz

 

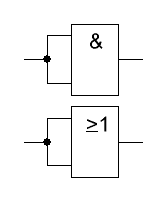Die Idempotenz besagt, dass, wenn beide Eingänge eines UND oder ODER-Gatters zusammengelegt werden, dass sich der Eingang gleich am Ausgang widerspiegelt.

Auch hier findet diese Schaltungsvariante hin und wieder in der Praxis Anwendung. Die Gründe sind die Gleichen wie schon beim Involutionsgesetz.

Es gibt aber noch eine Schaltungsvariante, welche eine ähnliche Auswirkung wie die beiden letzten Schaltungsgesetze haben.

 

 

Identitätsgesetz

 

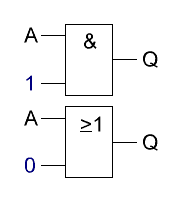Auch beim Identitätsgesetz, oder auch Neutralitätsgesetz genannt, wird der Eingang gleich zum Ausgang weiter geleitet. Hier wird nur der entsprechende zweite Eingang mit einem festen Signal versehen. Bei einem UND-Gatter ist dies ein 1-Signal und bei der ODER-Funktion entsprechend eine 0.

Werden die Signalpegel vertauscht, so hat man wohl wirklich eine Schaltungsvariante, wo es in der Praxis keinerlei Anwendung für gibt.

 

 

Extremalgesetz

 

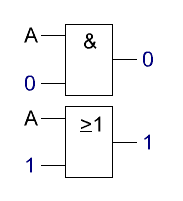Im Extremalgesetz, oder auch Annihilator oder Annulator, ist das Ergebnis immer ein fester Pegel. Unabhängig vom Eingangssignal. Bei einer UND-Verknüpfung trägt der Ausgang immer 0 während ein ODER-Gatter immer ein 1-Signal liefert.

Apropo Eingänge. Für viele ist es wohl schon selbstverständlich, aber auch das folgende Gesetz sollte man zumindest schon einmal gehört haben.

 

 

Kommutativgesetz

 

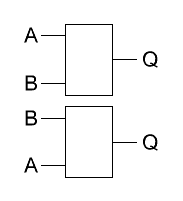Durch dieses Gesetz, welches auch häufig unter dem Namen Vertauschungsgesetz zu finden ist, verbirgt sich die Tatsache, dass man bei Logik-Gattern die Eingänge beliebig tauschen kann. Es also keine Rolle spielt, welche Signale an welche Eingänge des Gatters gelegt werden.

Dies ist insbesondere bei dem Entwurf von Platinen-Layouts interessant, da man hier sich nicht zwingend auf einen Eingang festlegen muss, sondern diese so beschalten kann, wie es im Layout am günstigsten ist.

 

 

Absorptionsgesetz

 

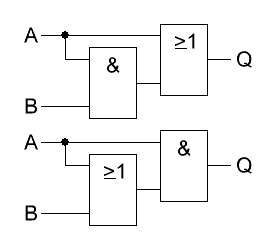Findet man in einer Schaltung diese Variante, so kann man diese beiden Gatter und die Zuleitung des Eingangs-Signal B, in der Regel, ersatzlos streichen. Denn, bei diesem Schaltungs-Gesetz heben sich beide Gatter gegenseitig auf und machen auch das zweite Eingangssignal überflüssig. Der Ausgang Q führt hier immer das Signal des Eingangs A.

Aber auch beim nächsten Gesetz ist die praktische Anwendung fragwürdig.

 

 

Komplementärgesetz

 

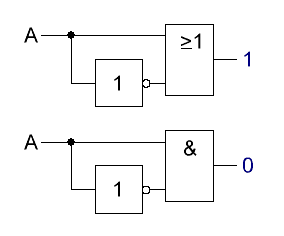Hier ergibt der Ausgang immer 1, bei einem ODER-Gatter, oder immer ein 0-Signal bei der UND-Funktion.

Es gibt natürlich auch noch sinnvollere Schaltungsgesetze.

 

 

De Morgan Gesetz

 

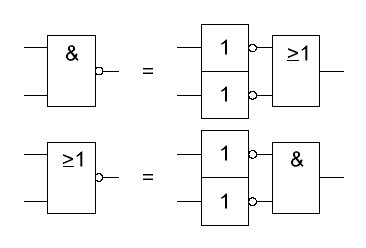Das De Morgan Gesetz besagt, dass man ein UND-NICHT-Gatter durch ein ODER-Gatter mit invertierten Eingängen oder ein ODER-NICHT-Gatter durch ein UND-Gatter mit invertierten Eingängen ersetzen kann.

Bei den nächsten Gesetzen werden Schaltungsvarianten mit 3 Eingängen beschrieben.

 

 

Assoziativgesetz

 

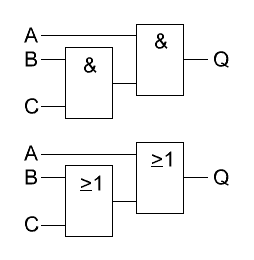Hat man nur UND oder ODER-Gatter mit je 2 Eingängen zur Verfügung, benötigt aber mindestens 3 Eingänge, so kann man das Assoziativgesetz, oder auch Verknüpfungsgesetz oder auch Verbindungsgesetz, anwenden.

Hier kann man die Gatter so verschalten als wären es Gatter mit 3 oder mehr Eingängen.

 

 

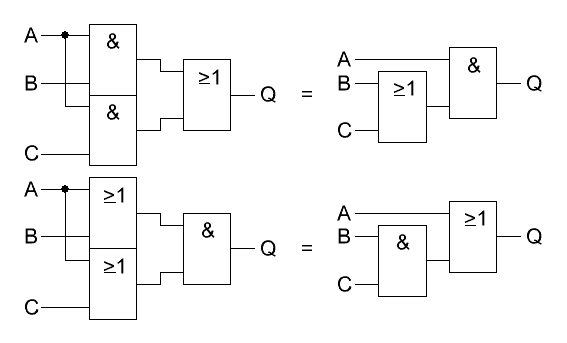Distributivgesetz

 

Die nebenstehende Schaltungsvariante ist recht häufig anzutreffen und lässt sich, dank des Distributivgesetzes, gut vereinfachen. So spart man jeweils ein UND oder ODER-Gatter ein.

 

 

Zurück zur Auswahlseite            Zur Hauptseite