Die Spezialität eines Mikroprozessors gegenüber einer
normalen digitalen Schaltung ist es, dass dieser Berechnungen und logische
Verknüpfungen ausführen und auch den weiteren Programmablauf vom Ergebnis dieser
Operation abhängig gemacht werden kann.
Eines der wichtigsten Kernelemente einer CPU ist die
ALU (Arithmetical Logical
Unit = Arithmetisch logische Einheit). Hier werden
Berechnungen durchgeführt und auch logische Verknüpfungen finden in der ALU
statt. In unserer ALU können neben Addition und Subtraktionen auch die logischen
Verknüpfungen Und, Oder und Nicht ausgeführt werden. ALUs in modernen
Prozessoren können weit mehr aber das würde hier den Bereich sprengen. Das
Grundprinzip ist jedoch ähnlich dem, was wir hier entwerfen.
Eine ALU kann unter anderem Addition durchführen.
Hierzu benötigen wir erst einmal einen Volladdierer. Wir können hier auf einen
fertigen Baustein zurück greifen. Es ist der
 4008. Wer
nicht genau weiß, was ein Volladdierer ist, dem empfehle ich den Lehrgang
4008. Wer
nicht genau weiß, was ein Volladdierer ist, dem empfehle ich den Lehrgang
 Addierer - Digitale Mathematik.
Der 4008 kann 2 4 Bit Zahlen addieren. Da wir hier ein 4-Bit-Prozessor aufbauen
wollen, reicht dieses IC also aus.
Addierer - Digitale Mathematik.
Der 4008 kann 2 4 Bit Zahlen addieren. Da wir hier ein 4-Bit-Prozessor aufbauen
wollen, reicht dieses IC also aus.
Für die 2 Eingabe-Zahlen werden 2 Eingabe-Einheiten
benötigt. Das Ergebnis stellen wir auf einer Ausgabeeinheit dar. Somit ergibt
sich dann der folgende Aufbau für den 4008:
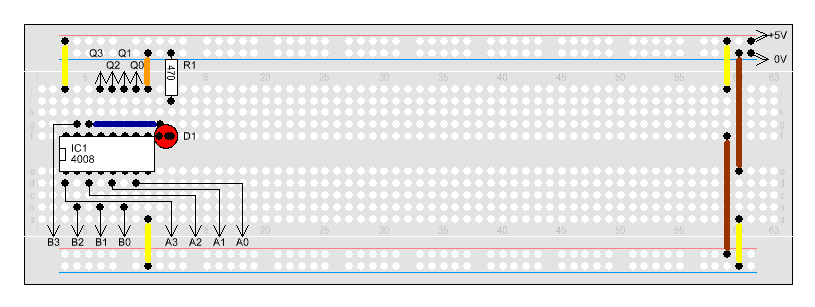
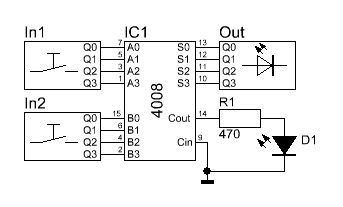 Nun
kann man mit Hilfe der beiden Eingabeeinheiten 2 Zahlen miteinander
addieren. Das Additionsergebnis wird binär auf der Ausgabeeinheit
angezeigt. Nun
kann man mit Hilfe der beiden Eingabeeinheiten 2 Zahlen miteinander
addieren. Das Additionsergebnis wird binär auf der Ausgabeeinheit
angezeigt.Leuchtet die LED D1 auf,
hat das Rechenergebnis einen Überlauf erzeugt. Dies bedeutet, dass das
Rechenergebnis größer als 15 ist, welches unser Addierer nicht mehr
darstellen kann. In so einem Fall, zeigt das IC dies an seinem
Carry-Ausgang an. Die Leuchtdiode wird angesteuert.
Das Carry-Signal wird in späterer
Entwicklung noch äußerst wichtig werden. Aber vorerst begnügen wir uns
nur mit der Anzeige. |
So gut die Addition mit der letzten Schaltung auch
funktioniert, so hat diese doch einen schweren Nachteil. Wir erhalten nur ein
Rechenergebnis, so lange wir die zu berechnenden Werte angelegt haben. Ändern
wir die Eingaben, ändert sich auch sofort das Ergebnis.
Für einen Prozessor ist dies aber nicht nutzbar. Hier
liegen die zu berechnenden Werte kurz am Datenbus an. Wir müssen also dafür
sorgen, dass die Werte erhalten bleiben, nachdem die Werte kurzfristig am
Datenbus anlagen.
Aber für solche Situation bietet die
Digital-Elektronik eine ganze Menge Bausteine an. Diese nennen sich Register.
Register sind im Grunde mehrere D-FlipFlops, bei denen der Takteingang
zusammengefasst wurde. Im Lehrgang
 Flip Flops - Sie vergessen nie
werden übrigens D-FlipFlops beschrieben, falls dies
noch jemand einmal nachlesen möchte.
Flip Flops - Sie vergessen nie
werden übrigens D-FlipFlops beschrieben, falls dies
noch jemand einmal nachlesen möchte.
Hier soll ein Register-Baustein vom Typ
 4076
verwendet werden. Dieser enthält ein 4 Bit-Register welches noch mit einigen
Extras ausgestattet ist. In diesem Moment interessiert uns nur die eigentliche
Register-Funktion.
4076
verwendet werden. Dieser enthält ein 4 Bit-Register welches noch mit einigen
Extras ausgestattet ist. In diesem Moment interessiert uns nur die eigentliche
Register-Funktion.
Mit Hilfe der Register können wir den Addierer nun so
ergänzen, dass dieser an ein Datenbus angeschlossen werden kann. Hierzu wird nun
das erste Eingabe-Board zum simulierten Datenbus. Von der 2. Eingabeeinheit
benötigen wir jetzt nur noch 2 Signale. Wir fügen die Register nun zum Addierer
hinzu:
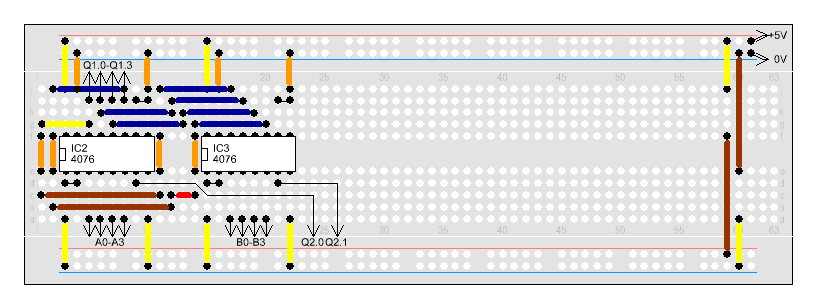
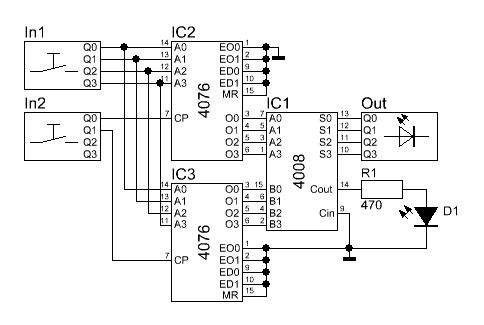 Wird
die Schaltung in Betrieb genommen, kann man nun am 1. Eingabe-Board
diverse Werte einstellen. Am Rechenergebnis geschieht nichts. Der
Addierer wird jetzt erst aktiv, wenn wir Werte in die Register
übernehmen. Wird
die Schaltung in Betrieb genommen, kann man nun am 1. Eingabe-Board
diverse Werte einstellen. Am Rechenergebnis geschieht nichts. Der
Addierer wird jetzt erst aktiv, wenn wir Werte in die Register
übernehmen.Hierzu müssen wir
entweder den Taster von Q2.0 vom 2. Eingabe-Board oder den Taster Q2.1
betätigen. Soll eine komplette Berechnung durchgeführt werden, so sind
folgende Schritte nötig. |
-
Einstellen des ersten Wertes auf der 1. Eingabeeinheit.
-
Betätigung des 1. Tasters des 2. Eingabe-Boards (Q2.0) um den eingestellten Wert
in IC2 (Register A) zu laden.
-
Einstellen des zweiten Wertes auf der 1. Eingabeeinheit.
-
Betätigung des 2. Tasters des 2. Eingabe-Boards (Q2.1) um den eingestellten Wert
in IC3 (Register B) zu laden.
Das Rechenergebnis kann nun an der Ausgangsanzeige
abgelesen werden.
Diese Bedienabfolge finden wir später auch in den zu
definierenden Assemblerbefehlen wieder. Um eine 4-Bit Addition durchzuführen,
könnte unsere Befehlsabfolge später so aussehen:
| LDA |
Wert |
; Lade Register A mit Wert (LoAD) |
| ADD |
Wert |
; Lade Register B mit Wert und zeige
Additionsergebnis |
Das addieren klappt ja schon ganz gut. Nur, soll
unsere ALU nicht nur addieren, sondern auch subtrahieren können. Aber wie
funktioniert das?
Um zu subtrahieren, müssen wir den Wert des
B-Registers negieren und auch den Carry-Eingang auf 1 setzen. Carry können wir
mit der neuen Steuerleitung für Addition/Subtraktion verbinden. Was aber noch
fehlt, ist ein Baustein, mit denen wir die Ausgabe des B-Registers bei Bedarf
negieren können. Bei einer Addition hingegen, soll das Register B unverfälscht
weiter gegeben werden.
Wenn wir uns die Logiktabellen der verschiedenen
Gatter ansehen, stoßen wir auf das Exklusiv-Oder-Gatter:
|
A |
B |
Q |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
1 |
0 |
An einem Eingang wird ein Bit des B-Registers
angeschlossen. Am zweiten Eingang schließen wir das Steuersignal für die
Addition/Subtraktions-Auswahl an. Wird nun die Addition gewählt (Steuersignal =
0) werden die Bits unverändert übertragen. Setzen wir jedoch das Steuersignal
auf 1 (Subtraktion) wird das Datenbit invertiert.
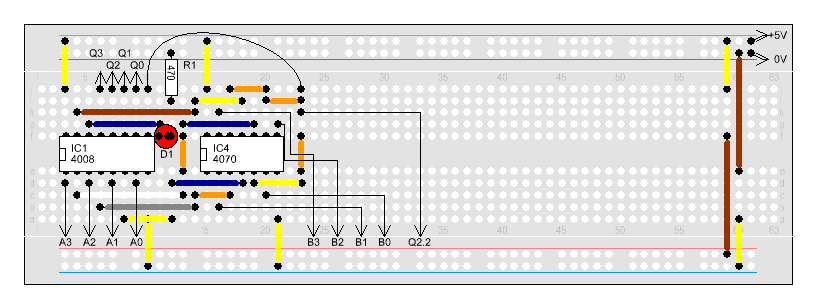
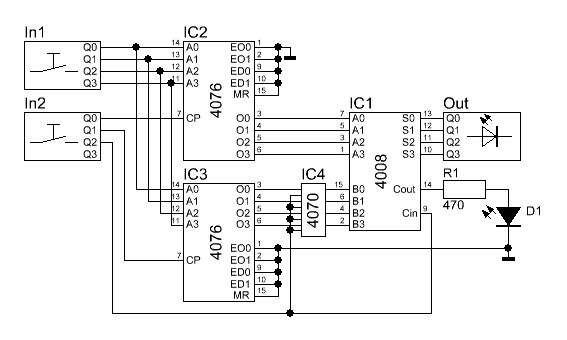 Jetzt
können wir mit Q2.2, also den 3. Taster des 2. Eingabeboards auswählen,
ob addiert oder subtrahiert werden soll. Jetzt
können wir mit Q2.2, also den 3. Taster des 2. Eingabeboards auswählen,
ob addiert oder subtrahiert werden soll.
Es muss noch beachtet werden, dass die
Carry-Anzeige (D1) sich bei der Subtraktion ebenso invertiert verhält.
Also ein Überlauf ist bei der Subtraktion dann vorhanden, wenn die LED
aus ist. |
Unseren späteren Assembler-Befehlsatz können wir nun
schon den 3. Befehl hinzufügen:
| LDA |
Wert |
; Lade Register A mit Wert (LoAD) |
| SUB |
Wert |
; Lade Register B mit Wert und zeige
Subtraktionsergebnis |
Die ALU hat nicht nur die Aufgabe, Werte zu addieren
oder zu subtrahieren, sondern sie soll auch die so genannten Flags erzeugen.
Flags sind Signale, welche bestimmte Zustände eines Rechenergebnisses anzeigen,
also Flagge bei bestimmten Ergebnisse zeigen.
Solche Flags werden benötigt um die CPU später
Entscheidungen treffen zu lassen. Erst dadurch erhält die CPU ihre
'Intelligenz'. Würde es die Flags nicht geben, wäre eine CPU nur eine einfache
Rechenmaschine.
Bei unserer CPU verwenden wir nur die beiden
wichtigsten Flags. Das Zero und das Carry-Flag. Vom letzteren haben wir ja
bereits schon was gelernt. Dieses muss zwar auch noch weiter aufbereitet werden,
ist aber im Grunde schon fertig. Daher kümmern wir uns jetzt erst einmal um das
Zero-Flag.
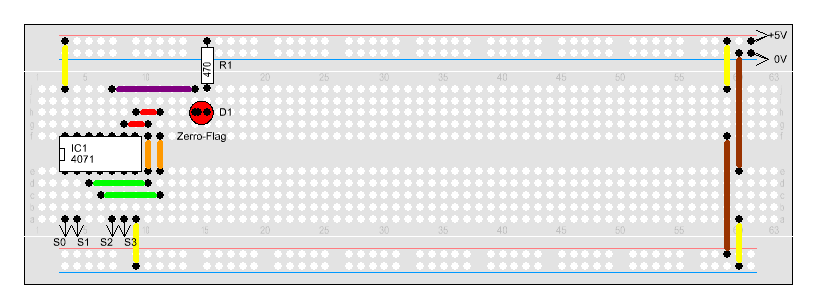
 Ein
Zero-Flag wird immer dann gesetzt, wenn das Ergebnis einer
Rechenoperation oder Logikfunktion 0 ergibt, wie der Name dieses Flags
ja bereits sagt. Ein
Zero-Flag wird immer dann gesetzt, wenn das Ergebnis einer
Rechenoperation oder Logikfunktion 0 ergibt, wie der Name dieses Flags
ja bereits sagt.Schauen wir uns
erst einmal an, wenn das Flag nicht gesetzt wird. Also sobald nur ein
Bit der 4 Eingänge S0-S3 1 ist, soll das Flag gelöscht sein.
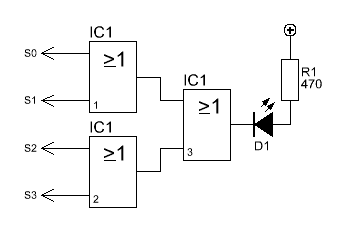
Um festzustellen ob eines der Bits 1 ist,
können wir Oder-Gatter verwenden. Zwar gebt der Ausgang ein 1-Signal
aus, wenn ein Bit gesetzt ist, da wir aber die Leuchtdiode 'falsch'
herum an das Oder-Gatter anschließen, leuchtet diese auf, wenn keines
der Eingänge 1 hat. Der Ausgang also 0 ist.
Nun haben wir hier aber ein Problem. Das
Zero-Flag wird zwar erzeugt. Bleibt aber nur so lange aktiv, bis der
nächste Assemblerbefehl abgearbeitet wird. Soll das Flag aber erst bei
späteren Befehlen ausgewertet werden, so müssen wir uns das Flag
'merken' bis es durch eine andere mathematische oder logische Operation
dieses wieder verändert wird. Es muss also ein D-FlipFlop dazu
geschaltet werden. |
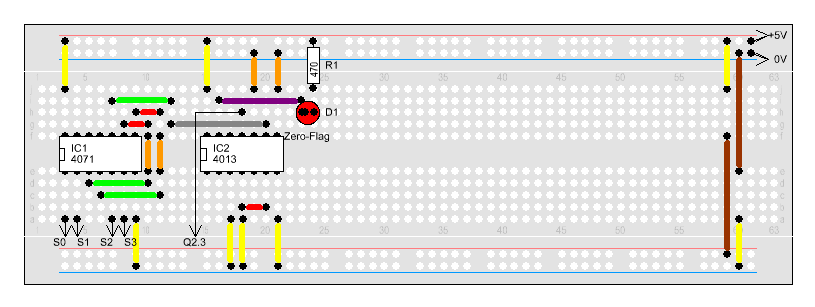
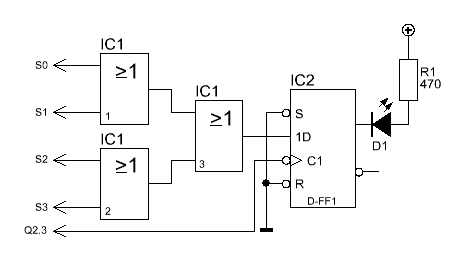 Zum
Speichern des Flags können wir ein schon bekanntes IC verwenden. Den Zum
Speichern des Flags können wir ein schon bekanntes IC verwenden. Den
 4013.
Um den Flag-Status in das FlipFlop zu übernehmen, brauchen wir noch eine
'Berechnung fertig'-Leitung. Hierfür verwenden wir den letzten freien
Taster des Q2-Eingebeboards.
4013.
Um den Flag-Status in das FlipFlop zu übernehmen, brauchen wir noch eine
'Berechnung fertig'-Leitung. Hierfür verwenden wir den letzten freien
Taster des Q2-Eingebeboards.Wird
nun eine Berechnung durchgeführt, muss anschließend noch kurz Q2.3
aktiviert werden, um das Zero-Flag zu übernehmen. Dieses steht nun, für
eine spätere Verwendung, zur Verfügung.
Durch dieses Flag haben wir jetzt schon
die Grundlage für eine Reihe der wichtigsten Befehle geschaffen.
Es können jetzt Vergleiche angestellt
werden. Hierzu wird einfach eine Subtraktion durchgeführt. Das Ergebnis
wird hierbei einfach ignoriert. Sind beide Werte gleich, ist das
Ergebnis ja 0, also das Zero-Flag gesetzt. Bei Ungleichheit ist das Flag
gelöscht. |
| CMP |
Wert |
; Vergleiche Register A mit Wert (CoMPare) |
Später können wir Befehle einsetzen, die das
Zero-Flag auswerten:
| JPE |
Adr. |
; Springe, wenn Zero gesetzt (Vergleich
ergab gleich, JumP
if Equal) |
| JPN |
Adr. |
; Springe, wenn Zero gelöscht (Vergleich
ergab ungleich, JumP
if Not equal) |
wird fortgesetzt ...